Question

What are the domain and the range of function ?()5 - 622 - 35 – 18(-0, -3) U(-3,)(-co, -3) UG-3, 6) (6, )(-0, 6) U6,0)(-o, -6) U(-6, 3)/(3, …)62, 0) (0, ) U (2, 00)(-0, 0) U 0,0)rangedomain>

Answer 1

We have to find the range and domain of f(x):

`f(x)=(x-6)/(x^2-3x-18)`

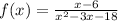
The domain is the set of values of x for which f(x) is defined.

f(x) will not be defined when the denominator is equal to 0. This means that the domain will be all the values of x but the roots of the denominator.

We can find the roots of the denominator as:

`\begin{gathered} x=(-(-3)\pm√((-3)^2-4*1*(-18)))/(2*1) \\ x=(3\pm√(9+72))/(2) \\ x=(3\pm√(81))/(2) \\ x=(3\pm9)/(2) \\ =>x_1=(3-9)/(2)=(-6)/(2)=-3 \\ =>x_2=(3+9)/(2)=(12)/(2)=6 \end{gathered}`

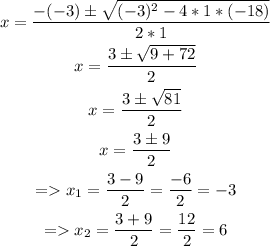
Then, as the domain will be all the values of x but x = -3 and x = 6, we can express it in interval notation as:

`D=(-\infty,-3)\cup(-3,6)\cup(6,\infty)`

Now, we have to calculate the range.

The range is the set of values that f(x) takes for the domain for which it is defined.

We can rearrange the function equation knowing the roots of the denominator:

`\begin{gathered} f(x)=(x-6)/((x+3)(x-6)) \\ f(x)=(1)/(x+3) \end{gathered}`

We can see that when x approaches infinity the value of f(x) approaches 0 from the positive side.

When x approaches minus infinity, f(x) approaches 0 from the negative side.

As there is no value of x that makes f(x) = 0, so y = 0 is not part of the range of f(x).

We have to exclude from the range the value that f(x) would have take for x = 6.

This is because f(x) is not defined for x = 6, although its simplified version, 1/x+3, is defined for x = 6.

In fact, f(x) has a discontinuity at x=6 that is a "hole", as it is not an asymptote.

We can calculate the value that f(x) would have taken for x = 6 as:

`f(6)=(1)/(6+3)=(1)/(9)`

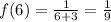
Then, the range is all the values of y = f(x) except y = 0 and y = 1/9.

Then, we can define the range in interval notation as:

`R=(-\infty,0)\cup(0,(1)/(9))\cup((1)/(9),\infty)`

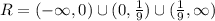
Answer:

Range --> (-∞, 0) ∪ (0,1/9) ∪ (1/9, ∞)

Domain --> (-∞, -3) ∪ (-3, 6) ∪ (6, ∞)