Question

Given right triangle ABC with altitude BD drawn to hypotenuse AC. If ÁC = 27and DC = 3, what is the length of BC?

Answer 1

Consider the triangle BDC.

Determine the length of side BD by using pythagoras theorem.

`\begin{gathered} (BD)^2=(x)^2-(3)^2 \\ =x^2-9 \end{gathered}`

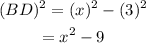
Consider triangle ABC.

Determine the length of side AB by using pythagoras theorem.

`\begin{gathered} (AB)^2=(27)^2-x^2 \\ =729-x^2 \end{gathered}`

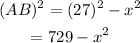
Consider the triangle ABD.

Determine the length of side BD by using the pythagoras theorem.

`\begin{gathered} (BD)^2)=(AB)^2-(AD)^2 \\ =729-x^2-(24)^2 \\ =153-x^2 \end{gathered}`

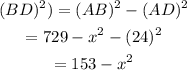
So,

`\begin{gathered} 153-x^2=x^2-9 \\ 153+9=2x^2 \\ x^2=(162)/(2) \\ x=\sqrt[]{81} \\ =\pm9 \end{gathered}`

The value of length can never be negative. So x = 9.

Thus length of side BC is 9 units.