Solution
- The bags of sand are going to be used to cover the expanse or area in form of a ring. This means that the area of the ring path must be the same area covered.
- This means that we must find the area of the ring. The area of the ring is simply gotten by subtracting the area of the smaller circle from that of the bigger circle.
- After getting this area, we can then assess how many 8yd² bags of sand can fill up this area.
- Thus, with the steps outlined above, we can proceed to solve the question.
- The area of a circle is given by:
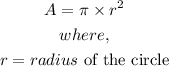
- Thus, we can find the areas of the small and large circles as follows:
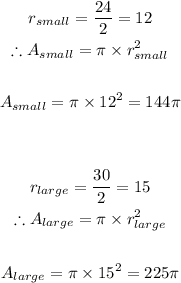
- Now that we have the areas of both circles, we can proceed to find the area of the ring path by subtracting as follows:
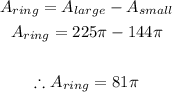
- This is the area of the ring path
- In order for us to know how many bags containing 8yds² of sand will fill up the ring path, we can simply divide the area of the ring path by the area of the bag of sand.
- That is,
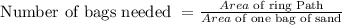
- The number of bags needed can thus be calculated as follows:
![\begin{gathered} Number\text{ of Bags needed }=(81\pi)/(8)=31.8086... \\ \\ \text{ Thus, the gardener needs about 31 bags of sand and little bit extra 0.8086... of a bag of sand.} \\ \\ \text{ We have been told that the answer must be a whole number, therefore, for the gardener to complete} \\ \text{ the work, he needs} \\ \\ (31+1)=32\text{ bags} \end{gathered}]()
- Thus, the number of bags needed is 32
Final Answer
The number of bags needed by the gardener is 32