Question

On each trial of an experiment, a subject is presented with a constant soft noise, which is interrupted at some unpredictable time by a noticeably louder sound. The time it takes for the subject to react to this louder sound is recorded. The following list contains the reaction times (in milliseconds) for the 17 trials of this experiment:

Answer 1

The first thing that we are going to do, is to order the results given by the experiment. We usually call these values as the data set: 232,152,186,193,175,231,202,229, 311,250, 212,236, 171,271,296,222,261. The data set ordered is given by

`{}{}\lbrace152,171,175,186,193,202,212,222,229,231,232,236,259,261,271,296,311\rbrace`

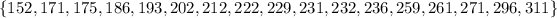
To find the 80th percentile, notice first that 80th percentile thinks of the 80% of your data, it means

`\begin{gathered} 0.8\text{ represents the 80\%, then } \\ 0.8(17)=13.6,\text{ where 17 is the size of your data set, or the cardinal of your set. } \end{gathered}`

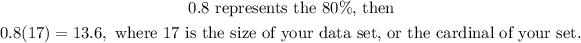
So, after counting place by place your ordered data set, you can notice that 261 is at the 14th position, then it will represent your 80th percentile.

80th percentile: 261, it means that 80% of the values of your data set are below 261

Now to find the 25th percentile we go ahead exactly as the 80th percentile. In this case

`\begin{gathered} 0.25\text{ represents the 25\%, then} \\ 0.25(17)=4.25,\text{ where 17 is the size of your data set.} \end{gathered}`

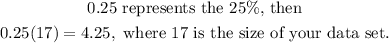
Then the 25th percentile= 193, it means that 25% of the values of your data set are below 193