Here, we want to prove that the right hand side of the equation equals the left hand side
We shall be moving from left to right to prove this
We proceed as follows;
Mathematically;
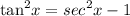
We replace this with the tan squared x in the bracket
Thus, we have the following;
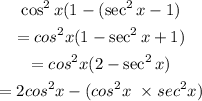
Kindly recall that;
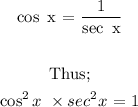
Hence, we have the following;
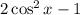
This is what we have on the left hand side
Let us simplify the right hand side too
This will be;
![undefined]()