EXPLANATION
Given the quadratic equation 4x^2 + 4y^2 -16x +24y=-27
As we already know, the circle equation with a radius r, centered at (a,b) is;
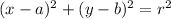
Dividing by coefficient of square terms: 4
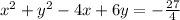
Group x-variables and y-variables together:
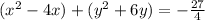
Convert x to square form:
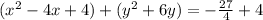
Convert to square form:
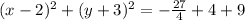
Refine -27/4+4+9
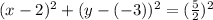
Therefore the circle properties are:
center: (a,b)=(2,-3), radius=5/2
The graph is as follows: