Question

A movie theatre's daily revenue follows a normal distribution, with an average daily revenue of $3,152. The standard deviation for the distribution is $1281. What is the probability that the theatre generates more than $4,000 in revenue on a randomly selected day?

Answer 1

0.2546

Step-by-step explanation

The movie theatre's daily revenue, X, is normally distributed with a mean of $3152 and a standard deviation of $1281.

We have to find the probability that the theatre generates more than $4000 in revenue on a randomly selected day,

`P(X>4000)`

To find this probability, we have to standardize X using the formula,

`Z=(X-\mu)/(\sigma)`

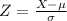
So the probability is,

`P\left((X-\mu)/(\sigma)\gt(4000-3152)/(1281)\right)=P(Z\gt0.66)`

Now, we have to look up this z-value in a z-score table. These tables usually show the area to the left of the z-score - this means that they show the probability for a z less than the z-score, so we have to find the complement,

`P(Z\gt0.66)=1-P(Z\lt0.66)`

In a z-score table,

So the probability is,

`P(X>4000)=1-P(Z\lt0.66)=1-0.7454=0.2546`

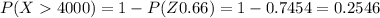
Hence, the probability that the theatre generates more than $4000 in revenue on a randomly selected day is 0.2546.