Question

In order to pay for college, the parents of a child invest $10,000 in a bond that pays 6% interest compounded semiannually. How much money will there be in 16 years? Round your answer to the nearest cent

Answer 1

The future amount for a compound interest can be calculated by the formula

`\text{ A= p(1+}(r)/(n))^(nt)`

Where A = Final amount

p = initial principal balance

r = interest rate

n = number of times interest is applied per period

t = number of times period elapses

For this question,

p = $10,000

r = 6%

The interest is compounded semi-annually, which means twice every year, hence

n= 2

t = 16

substituting the values into the formula. we have

`\begin{gathered} A\text{ = 10,000(1 +}(0.06)/(2))^{2\text{ x 16}} \\ A=10,000(1+0.03)^(32) \\ A=10000(1.03)^(32) \\ A=10.000(2.57508275) \\ A=25,750.8275 \\ \end{gathered}`

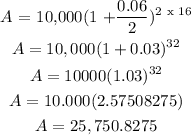
A = $25,750.

Hence, in 16 years, the bond will worth