Question

3. An exponential equation of the form, =⋅, passes through the points (12,147) and (18, 1029). A. Find this equation. Be sure to show your work.B. Using this equation, find y when x=8. Round to 3 decimal places.

Answer 1

We have an exponential function and 2 points that belong to that function.

We have to find the parameters "a" and "b" of the function.

We can start wit parameter b using both points. We divide the value of y for both points as:

`\begin{gathered} (y_2)/(y_1)=(a\cdot b^(x_2))/(a\cdot b^(x_1))=(b^(x_2))/(b^(x_1))=b^(x_2-x_1) \\ b=\sqrt[x_2-x_1]{(y_2)/(y_1)} \end{gathered}`

Replacing with the values (x1, y1) = (12, 147) and (x2, y2) = (18, 1029) we get the value of b:

`\begin{gathered} b=\sqrt[18-12]{(1029)/(147)} \\ b=\sqrt[6]{7} \\ b\approx1.383 \end{gathered}`

Now, we can use this result and one of the points to find the parameter a as:

`\begin{gathered} y_1=a\cdot1.383^(x_1) \\ 147=a\cdot1.383^(12) \\ a=(1.383^(12))/(147) \\ a=(49)/(147) \\ a=(1)/(3) \\ a\approx0.333 \end{gathered}`

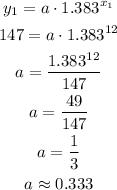
Now we can write the equation as:

`y=0.333\cdot1.383^x`

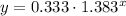
We can find the value of y when x=8 replacing x with 8 in the exponential function and calculating y:

`\begin{gathered} y(8)=0.333\cdot1.383^8 \\ y(8)=0.333\cdot13.387 \\ y(8)=4.457 \end{gathered}`

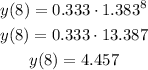
Answer:

A. The equation is y=0.333 * 1.383^x.

B. The value of y(8) is 4.457