• a) Given the points:
(x1, y1) ==> (k, 2)
(x2, y2) ==> (11, 14)
Slope, m = 2
To find the missing coordinate, k, use the slope formula below:

Input values into the formula to find k:
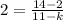
Let's solve for k.
Cross multiply:
b) Given the points:
(x1, y1) ==> (1, k)
(x2, y2) ==> (4, 1)
slope = -2
Let's use the method in question (a) to find k:

c) Given the points:
(x1, y1) ==> (3, 5)
(x2, y2) ==> (k, 9)
slope = 1/2
Let's use the method above to solve for k:
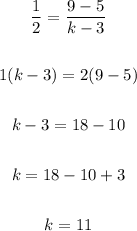
d) Given the points:
(x1, y1) ==> (-1, 4)
(x2, y2) ==> (-3, k)
slope = -1/2
Solve for k:

ANSWER:
a) k = 5
b) k = 7
c) k = 11
d) k = 5