Question

Prove that the quadrilateral with the coordinates L(-2,3), M(4,3), N(2,-2) and O(-4,-2) is a parallelogram.

Answer 1

The quadrilateral with the given coordinates has been proven to be a parallelogram.

How to prove the quadrilateral is a Parallelogram?

To prove that the quadrilateral with the coordinates L(-2,3), M(4,3), N(2,-2), and O(-4,-2) is a parallelogram, we can use the property that a quadrilateral is a parallelogram if both pairs of opposite sides are congruent and parallel.

First, we need to calculate the slopes of the sides and the lengths of the sides to show that they are parallel and congruent.

The slope of a line passing through two points (x1, y1) and (x2, y2) is given by the formula:

`m = ((y_(2) - y_(1)))/((x_(2) - x_(1)))`

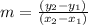
The length of a line segment with endpoints (x1, y1) and (x2, y2) is given by the formula:

d = √((x₂ - x₁)² + (y₂ - y₁)²).

The slopes of the sides are:

LM: (3 - 3)/(4 - (-2)) = 0

MN: (-2 - 3)/(2 - 4) = 5/2

NO: (-2 - 3)/(-4 - 2) = 5/2

OL: (3 - (-2))/(-2 - (-4)) = 5/2

The lengths of the sides are:

LM: √((4 - (-2))² + (3 - 3)²) = 6

MN: √((2 - 4)² + (-2 - 3)²) = 5

NO: √((-4 - 2)² + (-2 - 3)²) = 6

OL: √((-4 - (-2))² + (-2 - 3)²) = 5

We can see that the opposite sides LM and NO are parallel and congruent, and the opposite sides MN and OL are also parallel and congruent. Therefore, the quadrilateral with the given coordinates is a parallelogram.

Answer 2

LMNO is a parallelogram

Step-by-step explanation

Segments LM and NO are parallel, because they are both horizontal lines. Also, they are congruent because the horizontal distance between the endpoints is the same for both segments:

`\begin{gathered} d_(LM)=|-2-4|=|-6|=6 \\ d_(NO)=|2-(-4)|=|2+4|=6 \end{gathered}`

Then, segments LO and NM are parallel too. We can prove this with the slope

The slope is:

`\text{slope}=\frac{\text{rise}}{\text{run}}`

For both segments, the rise is 5 - which is the height of the parallelogram - and the run is 2. Therefore they have the same slope, so they are parallel.

Hence, LMNO is a parallelogram.