Question

Solve 2m^3 + 5m^2 - 13m -5=0, given -1/2 is a root

Answer 1

Step-by-step explanation:

Given;

We are given the following polynomial equation;

`2m^3+5m^2-13m-5=0`

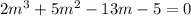
Required;

We are required to solve the polynomial given that -1/2 is a root.

Step-by-step solution;

We are already told that one of the roots of the equation is -1/2, that is;

`x=-(1)/(2)`

We can therefore divide the polynomial by this root to get the quotient which would be a quadratic equation. This is shown below;

Let us now go over the solution together.

Using the synthetic division method, we start by listing out the coefficients of each term in the polynomial and that is;

`\begin{gathered} Coefficients: \\ 2,5,-13,-5 \end{gathered}`

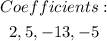
Next step, we take down the first coefficient, which is 2. Next we take the root (that is -1/2) and multiply this by the first coefficient.

That gives us,

`2*-(1)/(2)=-1`

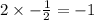
We write out the result directly under the next coefficient (that is 5) and add them together. That results in (5 - 1 = 4).

Next step, we multiply 4 by the root and we have;

`4*-(1)/(2)=-2`

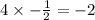
We write this result directly under the next coefficient (that is -13) and add them together. That gives us -15. Multiply this result by the root and we'll have;

`-15*-(1)/(2)=7(1)/(2)`

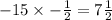
Write this result directly under the next coefficient and add up and we'll have 2 1/2 (or 2.5).

Note that we now have the new coefficients as;

`\begin{gathered} 2,4,-15 \\ Remainder\text{ }(5)/(2) \end{gathered}`

Therefore, the quotient is;

`2m^2+4m-15\text{ }+((5)/(2))/((m+(1)/(2)))=0`

Using the quadratic equation formula, we now have the other roots solved as follows;

`x=(-b\pm√(b^2-4ac))/(2a)`

Where the variables are;

`a=2,b=4,c=-15`

Inputing the variables into the quadratic formula above, will now give us;

`\begin{gathered} m_1=-(√(34))/(2) \\ m_2=-1+(√(34))/(2) \end{gathered}`

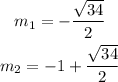
We now have the solution as;

ANSWER:

`m=-(1)/(2),-(√(34))/(2),-1+(√(34))/(2)`