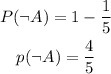The answer is:
Step-by-step explanation:
To calculate the probability of an event A occurring, we use the formula:
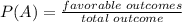
And, if P(A) is the probability of A occurring, the probability of A not occurring is:
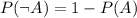
In this case, for a particular candidate to win a position, the total outcome is 10 people, and the favorable outcome is 2, for the 2 positions to be elected.
Then:
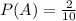
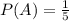
This is the probability of winning a position. The probability of not winning is: