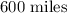Answer:
The number of miles Bill would have driven for the two plans to cost the same is;
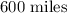
Step-by-step explanation:
Given that He can choose one of two plans.
Let C represent the cost and x represent the miles driven.
Plan 1;
an initial fee of $59.98 and costs an additional $0.13 per mile driven.

Plan 2;
an initial fee of $71.98 and costs an additional $0.11 per mile driven.
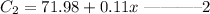
For the two plans to cost the same;
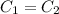
equating equation 1 to equation 2;
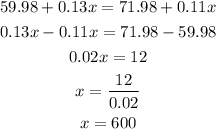
Therefore, the number of miles Bill would have driven for the two plans to cost the same is;