Question

Determine from the given points of two lines if the lines are parallel, perpendicular, or neither. Line a: (0,4) and (6,0)Line b: (4, -1) and (6,2)What is the slope of line a?Slope of line b?Are the slopes reciprocals?Are the lines parallel, perpendicular, or neither?

Answer 1

1. Slope of line a

Given the points (0,4) and (6,0)

Where: x1 = 0, x2 = 6, y1 = 4 and y2 = 0

`\text{slope}=(y2-y1)/(x2-x1)=(0-4)/(6-0)=(-4)/(6)=-(2)/(3)`

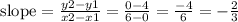
Answer: -2/3

2. Slope of line b

Given the points (4, -1) and (6,2)

Where x1 = 4, x2 = 6, y1 = -1 and y2 = 2

`\text{slope}=(2-(-1))/(6-4)=(2+1)/(2)=(3)/(2)`

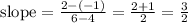
Answer: 3/2

3. Two slopes are reciprocal if the multiplication of both is equal to -1. Therefore, multiply the slopes:

`\begin{gathered} \text{slope a}* slope\text{ b = 1} \\ -(2)/(3)*(3)/(2)=1 \\ (-2*3)/(3*2)=1 \\ (-6)/(6)=1 \\ -1\\e1 \end{gathered}`

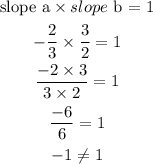
Since the multiplication of the two slopes is -1, the slopes are not reciprocal.

Answer: No, they are not reciprocals

4. Lines with the same slope are parallel and if the slope of one line is the negative reciprocal of the second line, then they are perpendicular.

In this case, the slopes are -2/3 and 3/2, therefore:

`-(2)/(3)*(3)/(2)=-(2*3)/(3*2)=-(6)/(6)=-1`

This means that the lines are perpendiculars.

Answer: Perpendicular