Question

Question is down below .You just have to fill in the blanks

Answer 1

Given the equations of the circles:

`\begin{gathered} x^2+y^2=4 \\ \\ x^2+y^2=1 \end{gathered}`

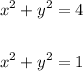
a. You can identify that they are written in this form:

`x^2+y^2=r^2`

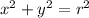
That is the form of the equation of radius "r" whose center is at the Origin.

In this case, you can identify that:

- For the first circle:

`r^2=4`

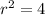
Then, solving for "r", you get that its radius is:

`r=\sqrt[]{4}=2`

- For the second circle:

`r^2=1`

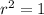
Therefore, its radius is:

`r=\sqrt[]{1}=1`

Hence, knowing their centers at the Origin and knowing the radius, you can graph the circles on the same Coordinate Plane:

Notice that the larger circle is:

`x^2+y^2=4`

And the small circle is:

`x^2+y^2=1`

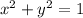
b. Now you have to find the image of any point on the larger circle under the following transformation:

`(x,y)\rightarrow((1)/(2)x,(1)/(2)y)`

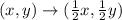
Choosing this point on the larger circle:

`(2,0)`

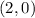
You need to multiply each coordinate by the following scale factor (based on the given rule), in order to find its image:

`k=(1)/(2)`

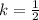
Therefore, you get:

`(2,0)\rightarrow(2\cdot(1)/(2),0\cdot(1)/(2))=(1,0)`

You can plot both points on the Coordinate Plane:

c. By analyzing the graph and the points plotted, you can conclude that the small circle is obtained by dilating the larger circle, using the Origin as the Center of dilation and this scale factor:

`k=(1)/(2)`

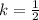
Since is smaller than the larger circle, it is a reduction of it.

Hence, the answers are:

a.

The larger circle is:

`x^2+y^2=4`

The small circle is:

`x^2+y^2=1`

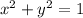
b.

`(1,0)`

c. The small circle is a reduction of the larger one using the origin as the center and a scale factor of:

`(1)/(2)`