Question

Bea is asked to graph this system of equations: 8x - 6y= 3 -3y + 4x = 4 How many times will the lines intersect?

Answer 1

Given the system of equations:

8x - 6y = 3

-3y + 4x = 4

To find how many times the lines will intersect. let's solve the system of equation using substitution method.

8x - 6y = 3 ........................................1

-3y + 4x = 4 ......................................2

From equation 1, make x the subject:

8x - 6y = 3

8x = 3 + 6y

`\begin{gathered} x=(3)/(8)+(6)/(8)y \\ \\ x=(3)/(8)+(3)/(4)y \end{gathered}`
`\text{Substitute (}(3)/(8)+(3)/(4)y)\text{ for x in equation 2}`

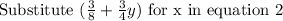
We have:

`\begin{gathered} -3y+4((3)/(8)+(3)/(4)y)=4 \\ \\ -3y+(3)/(2)+3y=4 \\ \\ \end{gathered}`

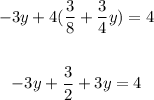
Multiply through by 2 to eliminate the fraction:

`\begin{gathered} -3y(2)+(3)/(2)(2)+3y(2)=4(2) \\ \\ -6y+3+6y=8 \end{gathered}`

`\begin{gathered} -6y+6y=8-3 \\ \\ 0=5 \end{gathered}`

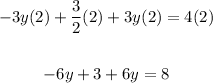
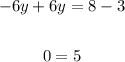
Since we have 0 = 5, it means the system of equations has no solution.

Therefore, the lines will not intersect, because this system has no solution.

ANSWER:

A. The lines will not intersect, because this system has no solution.