Question

6.) A company produces a container that is 10 inches tall and weighs 4.6 pounds. Unfortunately,this company can no longer afford to make this container. It plans to produce a smallercontainer, which is similar to the original. The dimensions of the new container will be 75% ofthe original dimensions.a.) What is the linear scale factor between the original and the new containers?Use old dimension/new dimension as the scale factorb.) How tall is the new container?c.) How much will the new container weigh?

Answer 1

Answer:

a) scale factor = 1.33

b) The new container's height = 7.5 inches

c) The new container will weigh = 3.45 pounds

Step-by-step explanation:

Given:

The height of the container = 10 inches

mass of the container = 4.6 pounds

The dimensions of the new container will be 75% of the original dimensions

To find:

a.) What is the linear scale factor between the original and the new containers?

b.) How tall is the new container?

c.) How much will the new container weigh?

From our question, the new dimensions will be 75% of the original. This means we are scaling down.

`scale\text{ factor = }\frac{old\text{ dimension}}{new\text{ dimension}}`
`\begin{gathered} new\text{ height = 75\% \lparen10\rparen = 0.75\lparen10\rparen = 7.5 inches} \\ \\ scale\text{ factor = }\frac{old\text{ height}}{new\text{ height}} \\ scale\text{ factor = }(10)/(7.5) \\ scale\text{ factor = 1.33} \end{gathered}`

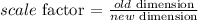
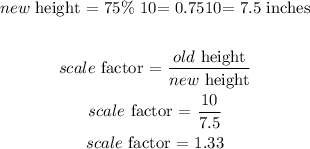
b) The new container's height = 75% (old height)

The new container's height = 0.75 (10) = 7.5 inches

c) The weight/mass of the new container = 75% (old weight)

The new container will weigh = 0.75(4.6)

The new container will weigh = 3.45 pounds