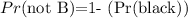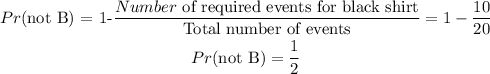Question

In a dresser are 7 blue shirts, 3 red shirts, and 10 black shirts. - what is the probability of randomly selecting a red shirt?- what is the probability that a randomly selected shirt is not black?

Answer 1

Step 1

Write the expression for the probability of an event.

`\text{Probability of an event A =}\frac{Numberof\text{ required events}}{\text{Total number of events}}`

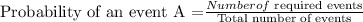
Where

Number of required events for red shirts = 3 shirts

Number of required events for black shirts= 10 black shirts

Number of required events for blue shirts = 7 blue shirts

Total number of required events = 20 shirts

Step 2

Find the probability of randomly selecting a red shirt(R).

`Pr(R)=\frac{Number\text{ of required events for red shirt}}{\text{Total number of required events}}=(3)/(20)`

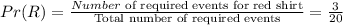
Step 3

Find the probability of randomly selecting a shirt that is not black(not B).

`Pr(\text{not B)=1- (Pr(black)) }`
`\begin{gathered} Pr(\text{not B) = 1-}\frac{Number\text{ of required events for black shirt}}{\text{Total number of events}}=1-(10)/(20) \\ Pr(\text{not B)}=(1)/(2) \end{gathered}`