ANSWER:
66666.67 km/hr
Explanation:
Given:
Distance (d) = 100000 km
Time (t) = 1.5 hr
We can calculate the speed knowing that it is the quotient between the distance and the time, just like this:
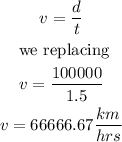
The velocity of the plane is 66666.67 kilometers per hour