In the given similar traingles ABC and MNO
From the properties of similar triangle :
The ratio of corresponding sides of similar triangle are always equal
In the triangle ABC and MNO
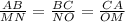
In the given figure, we have : AB = 12, BC = 10, NO = 3
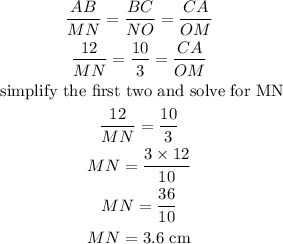
In triangle ABC apply pythagoras for the side AC
![\begin{gathered} \text{ Hypotenuse}^2=Perpendicular^2+Base^2 \\ AC^2=AB^2+BC^2 \\ AC^2=12^2+10^2 \\ AC^2=144\text{ + 100} \\ AC^2=244 \\ AC=\sqrt[]{244} \\ AC=15.62\text{ cm} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ywvmtukqt1797xj90zy1da1yixksaqrnxs.png)
Now apply the corresponding ratio :
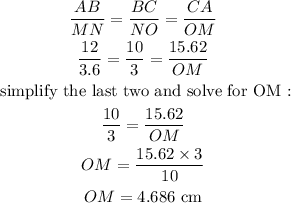
OM = 4.69 cm
In triangle MNO
MN = 3.6 cm, NO = 3 cm, OM = 4.69 cm
Answer :
MN = 3.6 cm,
NO = 3 cm,
OM = 4.69 cm