Question

A business executive bought 40 stamps for $9.60. The purchase includes 25 cents and 20 cents stamps. How many f each type of stamp were bought?

Answer 1

Step-by-step explanation:

We can write a system of linear equations with this information.

• x: number of 25 cent stamps

,

• y: number of 20 cent stamps

The system is:

`\begin{gathered} x+y=40 \\ 0.25x+0.20y=9.60 \end{gathered}`

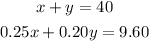
Solving using the substitution method, we first clear y from the first equation:

`y=40-x`

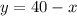
Replace into the second equation:

`0.25x+0.20(40-x)=9.60`

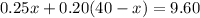
And solve for x:

`\begin{gathered} 0.25x+0.20*40-0.20x=9.60 \\ 0.05x+8=9.60 \\ 0.05x=9.60-8 \\ x=(1.6)/(0.05)=32 \end{gathered}`

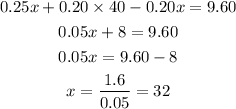
Finally, replace x = 32 into the equation for y we cleared before to find the value of y:

`y=40-x=40-32=8`

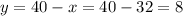
Answer:

He bought:

• 32, ,25-cent stamps

,

• 8 ,20-cent stamps