Question

A message in a bottle is floating at the top of the ocean in a periodic manner the time between periods and maximums heights is 26 seconds and the average height of the bottle is 12 feet the bottle moves in a manner such that the distance from the highest and lowest point is 6 feet a cosine function can model the movement of the message in a bottle in Malaysian to the height Part A. Determine the amplitude and period of the function that could model the height of the message in the bottle as a function of time T Part B. assume that at T equals zero the message in a bottle is at its average height and moves upwards after what is the equation of the function that could represent the situation based on the graph of the function after how many seconds will it reach its lowest height

Answer 1

Part A.

We are asked to determine the amplitude and the period of the movement of the bottle. The amplitude is defined as half the distance between the highest and lowest points of the graph. Since that distance is given to be 6 feet, we have that the amplitude is:

`A=(6ft)/(2)=3ft`

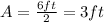
Therefore, the amplitude is 6ft.

The period of the movement is given to be 26 seconds.

Part B. We are asked to determine a cosine function that models the movement. A cosine function has he following general form:

`y=Acos(bt+c)+d`

"A" is the amplitude and, in this case, is equal to 3 ft, therefore:

`y=3cos(bt+c)+d`

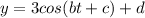
The value of "d" is related to theperiod by the following relationshiop:

`b=(2\pi)/(T)`

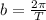
Where "T" is the period. Since the period is 26, we have:

`b=(2\pi)/(26)=(\pi)/(13)`

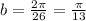
Therefore, the function is:

`y=3cos((\pi)/(13)t+c)+d`

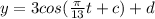
The valu of "d" is the averagae height of the motion, therefore, "d = 12ft":

`y=3cos((\pi)/(13)t+c)+12`

To determine the value of "c" we use the fact that the function starts at the average height., therefor:

`t=0,y=12`

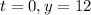
Substituting we get:

`12=3cos((\pi)/(13)(0)+c)+12`

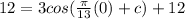
We can cancel out the 12:

`0=3cos(c)`

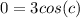
We divide both sides by 3:

`cos(c)=0`

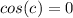
The values that satisfy this are:

`c=(\pi)/(2),-(\pi)/(2)`

We will take the negative valuesince rwe are given that the motion goes upwards after the initial position. Therefore, we get:

`y=3cos((\pi)/(13)t-(\pi)/(2))+12`

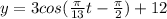
And thus we get the function of the motion.

The graph is the following:

Therefore, according to the graph, the lowest height is eached atfter 19.5 seconds.