She wants to earn a salary that is $2,700 or more, so we can write this as:
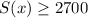
Her salary S(x) depends on x, the amount of sales she makes.
If she sells $100 she will have a comission of 3%, what means a 0.03*100 = $3 addition to her salary.
This can be generalized as 0.03*x for the commissions.
Then, she had her salary composed by a fixed salary ($2,000) and a variable salary (0.03*x).
Then we can write S(x) as:
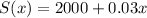
Joining with the inequality above, we would have:
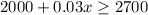
We can solve this inequality for the amount of sales x as:
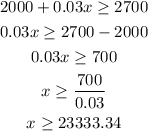
Answer:
The inequality to start solving the problem is 2000+0.03x>=2700.
The variable x represents the amount of sales she makes.
The value 0.03 is the commission rate in decimals.
The amount of sales she has to make to earn at least $2,700 is $23,333.34.