Question

You are moving a 150 kg block along a horizontal floor. You apply a force of 900 Newtons to the right. As the block slides, the floor exerts a friction force. What is the resulting acceleration of the block (in m/s)?

Answer 1

a = (6 - 9.8μ) m/s²

Step-by-step explanation

A free-body diagram of this situation is:

Since no coefficient of friction is provided, we can suppose that the force applied to the box is enough to actually move it - i.e. it is greater than the static friction force.

To find the acceleration of the block, we have to use the Second Newton's law of motion:

`F_{\text{net}}=m\cdot a`

The block won't move vertically, so we have to consider the horizontal forces:

`F-F_f=m\cdot a`

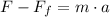
The friction force is the product of the normal force Fn and the coefficient of friction μ:

`F_f=F_N\cdot\mu`

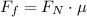
And the normal force, since the block doesn't move vertically, equals in magnitude to the weight of the block:

`F_N=F_g=m\cdot g_{}`

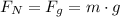
Therefore, the second expression, replacing with these two expressions, is:

`F-m\cdot g\cdot\mu_{}=m\cdot a`

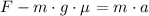
Solving for a:

`a=(F-m\cdot g\cdot\mu)/(m)=(F)/(m)-g\cdot\mu`

g is the acceleration of gravity, often used with the value 9.8 m/s². F = 900N and m = 150kg:

`\begin{gathered} a=(900)/(150)-9.8\cdot\mu \\ a=(6-9.8\mu)m/s^2 \end{gathered}`