Question

Here is a scatter plot that shows the years when some used cars were madeand their prices in 2016, together with the graph of a linear model for therelationship between year and price.

Answer 1

The positive slope, estimated to be approximately 1000, indicates that, on average, the price of used cars increases by $1000 per year according to the linear model.

1. The slope of the linear model can be determined by examining the trend of the scatter plot. If the prices generally increase as the years go up, the slope is positive; if the prices decrease, the slope is negative. In this case, since the scatter plot represents used car prices over the years, we observe an upward trend from the given data points. Therefore, the slope is positive.

2. To estimate the slope, we can select two points from the data and use the formula:
`\[\text{Slope} = \frac{\text{Change in Price}}{\text{Change in Year}}.\]`

Considering the points (2007, 7000) and (2015, 21000), the change in price is 21000 - 7000 = 14000 and the change in year is 2015 - 2007 = 8. Thus, the slope is
`\((14000)/(8) = 1750\).`

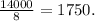
3. The selected value closest to the slope is 1000 (option a). The positive slope of 1000 implies that, on average, the price of used cars increases by $1000 per year. Therefore, the linear model suggests that, for each additional year, the price of a used car tends to rise by $1000.

Answer 2

1. Since the price increases as a function of the years, we can conclude it is a positive slope.

2.

`\begin{gathered} (x1,y1)=(2012,15000) \\ (x2,y2)=(2015,18000) \\ m=(18000-15000)/(2015-2012)=(3000)/(3)=1000 \end{gathered}`

The slope is approximately 1000

3.

This means the price of the used cars increase by 1000 every year