Question

A bag contains 10 marbles: 2 are grean, 5 are red, and 3 are blue. Milan chooses a marble at random, and without putting it back, chooses another one atrandom. What is the probability that both marbles he chooses are red? write your answer as a fraction in simplest form.0х?ContinueSubmit A

Answer 1

The probability that an event A occurs (P(A)) is:

`P(A)=\frac{\text{ number of favorable outcomes of A}}{\text{ number of total outcomes}}`

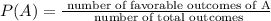
To solve this question, follow the steps below.

Step 01: Calculate the probability the first marble is red.

Number of favorable outcomes = 5 (5 red marbles).

Number of total outcomes = 10 (10 marbles).

Then, P(red₁):

`P(\text{red}_1\text{)}=(5)/(10)=(1)/(2)`

Step 02: Calculate the probability the second ball is also red.

Now, let's assume that 1 red ball was removed. Then,

Number of favorable outcomes = 4 (4 red marbles remained).

Number of total outcomes = 9 (number of total marbles remained).

Then, P(red₂):

`P(red_2)=(4)/(9)`

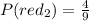
Step 03: Calculate the probability the first and the second marbles are red.

The probability both marbles are red is the product of both probabilities.

`\begin{gathered} P(\text{red)}=P(red_1)\cdot P(red_2) \\ P(\text{red)}=(1)/(2)\cdot(4)/(9) \\ P(\text{red)}=(4)/(18) \end{gathered}`

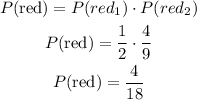
And dividing the numerator and denominator by 4:

`P(\text{red)}=((4)/(2))/((18)/(2))=(2)/(9)`

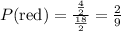
Answer: The probability that both marbles he chooses are red is 2/9.