Question

Please help, and let me know if you can't, I won't be upset

Answer 1

`(d^2y)/(dx^2)=4`

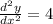
Step-by-step explanation

We want to find the second derivative of the function at the given point:

`2-xy-2y=0`

First, differentiate the function implicitly:

`0-y-x(dy)/(dx)-2(dy)/(dx)=0`

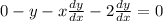
Next, differentiate the function implicitly a second time:

`\begin{gathered} -(dy)/(dx)-(dy)/(dx)-x(d^2y)/(dx^2)-2(d^2y)/(dx^2)=0 \\ -2(dy)/(dx)-(x+2)(d^2y)/(dx^2)=0 \\ -(x+2)(d^2y)/(dx^2)=2(dy)/(dx) \\ (d^2y)/(dx^2)=(2)/(-(x+2))(dy)/(dx) \end{gathered}`

From the first derivative, we have that:

`\begin{gathered} -y-(x+2)(dy)/(dx)=0 \\ -(x+2)(dy)/(dx)=y \\ (dy)/(dx)=(y)/(-(x+2)) \end{gathered}`

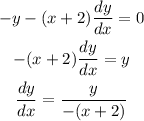
Substitute that into the second derivative:

`\begin{gathered} (d^2y)/(dx^2)=(2)/(-(x+2))*(y)/(-(x+2)) \\ (d^2y)/(dx^2)=(2y)/((x+2)^2) \end{gathered}`

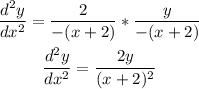
Now, substitute the values of the point given into the equation and simplify:

`\begin{gathered} (d^2y)/(dx^2)=(2(2))/((-1+2)^2) \\ (d^2y)/(dx^2)=(4)/(1^2) \\ (d^2y)/(dx^2)=4 \end{gathered}`

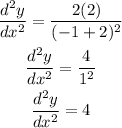
That is the answer.