Question

Need help SHOWING the work for this problem. The answer is already there

Answer 1

As given by the question

(1)

There are given that the equation:

`y=3x^2+7`

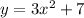
Now,

Put the value of y is 27 and x is 3 into the above equation to check the solution

So,

From the equation:

`\begin{gathered} y=3x^2+7 \\ 27=3(3)^2+7 \\ 27=3(9)+7 \\ 27=27+7 \\ 27\\e34 \end{gathered}`

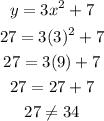
Hence, the answer is No.

Now,

(2):

From the equation:

`y=-3x^2`

Now,

The graph of the given equation is shown below:

According to the question,

There are given that negative values, that means -3.

So, the graph of the parabola is downwards from the origin.