Question

Suppose 45% of the people in a community use the emergency room at a hospital inone year, find the probability exactly 6 for a sample of 10 people. Use the binomialprobability formula. Write your answer with three decimal places.

Answer 1

Given

total number , n= 10

successful events , x = 6

probability of success, p =45% = 0.45

probability of failure , q = 1 - p = 1 - 0.45 = 0.55

Find

the probability exactly 6

Step-by-step explanation

Use binomial probability formula ,

`P(x)=^nC_xp^x(1-p)^(n-x)`

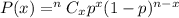
so ,

`\begin{gathered} P(x)=^(10)C_6(0.45)^6(0.55)^4 \\ \\ P(x)=(10!)/(6!4!)*0.00830376563*0.09150625 \\ \\ P(x)=0.159567755 \end{gathered}`

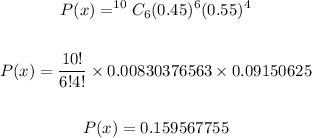
Final Answer

Probability of exact 6 = 0.160