SOLUTION
Let us represent this with a diagram for a better understanding
So from the diagram, let the shorter leg be x, then the longer leg will be x + 7
From Pythagoras theorem,
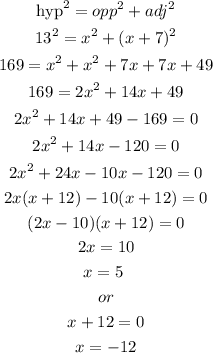
Since x cannot be negative, we go with x = 5
So the shorter leg x = 5 inches
The longer leg x + 7 = 12 inches
The hypotenuse is 13 inches