Question

About 2% of the population has a particular genetic mutation. 900 people are randomly selected.Find the mean for the number of people with the genetic mutation in such groups of 900. Round your answer to two decimal places._____.

Answer 1

We need to find the mean for the number of people with the genetic mutation in a group of 900.

We know that the probability of each person having that genetic mutation is 2%. Thus, this is a binomial distribution, with:

`p=2\%=(2)/(100)`

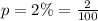
Therefore, for a number n of people, the mean μ is given by:

`\mu=n\cdot p`

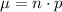
Thus, for n = 900, we have:

`\mu=900\cdot(2)/(100)=(900)/(100)\cdot2=9\cdot2=18`

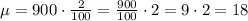
Answer: 18