Question

In a study of government financial aid for college students, it becomes necessary to estimate the percentage of full-time college students who earn a bachelor's degree in four years or less. Find the sample size needed to estimate that percentage. Use a 0.04 margin of error and use a confidence level of 95%. Complete parts (a) through (c) below.A). Assume that nothing is known about the percentage to be estimated.n= ___ (Round to the nearest integer)B.) Assume prior studies have shown that about 60% of full-time students earn bachelor's degrees in four years or less.n=____ (Round to the nearest interger)C.) Does the added knowledge in part (b) have much of an effect on the sample size?Yes or No

Answer 1

Given:

Margin of error = 0.04

Confidence level = 95%

Let's answer the following questions:

• (A). Assume that nothing is known about the percentage to be estimated.

Since we are to assume that nothing about the percentage is know, we have:

p = q = 0.5

E = 0.04

Given a 95% confidence interval, we have:

Significance level = 1 - 0.95 = 0.05

Using the z-table, for a two tailed test, we have:

`z_{(0.05)/(2)}=1.96`

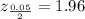
Hence, the sample size will be:

`\begin{gathered} n=pq(\frac{z_{(\alpha)/(2)}}{E})^2 \\ \\ n=(0.5)(0.5)((1.96)/(0.04))^2 \\ \\ n=0.25*2401 \\ \\ n=600.25\approx600 \end{gathered}`

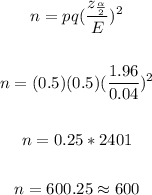
Therefore, the required sample size is 600

• (b,). Here, we have the following:

p = 60% = 0.60

q = 1 - p = 1 - 0.60 = 0.40

95% confidence interval, z = 1.96

E = 0.04

To solve for n, we have:

`\begin{gathered} n=(0.6)(0.4)((1.96)/(0.04))^2 \\ \\ n=576.24\approx576 \end{gathered}`

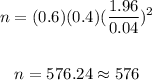
Here, the sample size is 576

(C).

No, the added knowledge in part B does not have much of an effect on the sample size.

It only slightly reduces the sample size.

ANSWER:

• (A). 600

,

• (B). 576

,

• (C). No, it only slightly reduces the sample size.