First, let's identify the slope of the given line by comparing it with the slope-intercept form of the linear equation:

Where m is the slope and b is the y-intercept.
From the given line, we have a slope of m = 3/4.
Parallel lines have the same slope, so the slope of the wanted equation is also m = 3/4.
Now, to find the equation, we can use the point-slope form of the linear equation:

Using the slope m = 3/4 and the given point (8, 18), that is, x1 = 8 and y1 = 18, we have:
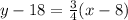
Therefore the correct option is the first one.