We want to write the equation of a line that is perpendicular to:
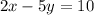
We remember that two perpendicular lines have opposite inverse slopes. This means that when we multiply the slopes of the two lines, we obtain -1. Thus, we will find the slope of the equation given by solving for y:
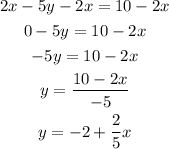
This means that the slope of the line given is 2/5. For finding a opposite inverse number to the one given, we interchange the numerator and the denominator, and we change its sign:
Thus, the slope of the perpendicular line should be:
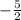
And we can choose its y-intercept. On this case, we will choose the y-intercept to be 0, and we get that an equation of a line that is perpendicular to 2x-5y=10 is:
