Question

Im an older woman and i could really use some help this math is new to meTwo angles are supplementary. One angle is 36° more than the other. Find the measures of the angles.

Answer 1

To solve this, we need to create a system of equations using the info provided by the problem.

Two supplementary angles are two angles that add up to 180º

If we call one angle x and the other y:

`x+y=180º`

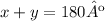
Next, one angle is 36º more than the other, we can write then:

`x+36º=y`

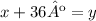
Now we have a system of equations. We can then use substitution to get the values of each angle. Substitution consist in substitute the value of one equation in to the other, since we know, by the second equation, that y = x + 36º, we can replace this value of y in the first eqaution:

`\begin{gathered} \begin{cases}x+y=180º \\ y=x+36º\end{cases} \\ x+x+36º=180º \end{gathered}`

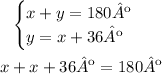
Then we can solve for x:

`\begin{gathered} x+x+36º=180º \\ 2x=180º-36º \\ x=(144º)/(2) \\ x=72º \end{gathered}`

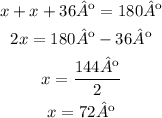
The measure of one of the angles is 72º. To find the measure of the other angle, we can go back to the first equation and substitute the value of x = 72º:

`\begin{gathered} \begin{cases}x+y=180º \\ x=72º\end{cases} \\ 72º+y=180º \end{gathered}`

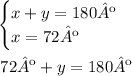
And solve for y:

`\begin{gathered} 72º+y=180º \\ y=180º-72º=108º \end{gathered}`

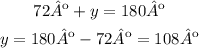
THe value of the other angle is 108º

Now we can verify if the values we gat are correct by using the second equation. Angle x plus 36º must to be equal to angle y:

`72º+36º=108º`

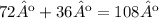
Thus, the answer we get is correct.