Since the tank is filled up to 3/4 of its maximum volume and this represents 14.4 liters of water, we have the following equation:

where V represents the total volume of the tank. Since we have the measure of the width and the length in cm, we can convert 14.4 in cm^3 to get the following:
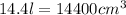
Now, we know that the formula for the volume of a rectangular prism is:

where w,l and h represent the width length and height respectively. Substituting the values that we have,we get the following equation:
![\begin{gathered} (3)/(4)V=14400 \\ \Rightarrow0.75w\cdot l\cdot h=14400 \\ \Rightarrow0.75(40)(20)h=14400 \\ \Rightarrow600h=14400 \\ \Rightarrow h=(14400)/(600)=24 \\ h=24\operatorname{cm} \end{gathered}]()
therefore, the height of the tank is 24 cm