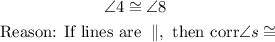Question

Use the given information to prove that ∠4 ≅ ∠8.

Answer 1

Given the image, we are asked to prove that

`\angle4\cong\angle8`

The solution can be seen below;

Step-by-step explanation

The sign in the middle of the angles above implies congruency. Two angles are congruent if and only if they have the same measure.

Taking a look at the image, we can see that line F and line G are two parallel lines that are cut by a transversal.

Now, the Corresponding Angles Postulate states that, when two parallel lines are cut by a transversal, the resulting corresponding angles are congruent

An example can be seen below;

From the image above, we can see that angles 4 and 8 are positioned in a similar manner in the question. This implies that they are corresponding angles.

Therefore;

Answer:

`\begin{gathered} \angle4\cong\angle8 \\ \text{ Reason: If lines are }\parallel,\text{ then corr}\angle s\cong \end{gathered}`