The question says that the product of two consecutives even integers is 120, wich give us the expression:
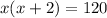
Developing the calculations, we end with the followed second degree equation:
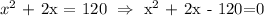
We can use Bhaskara's formula to find the roots, as follow:
![x=\frac{-2\pm\sqrt[]{2^2-4(1)(-120)}}{2*1}\text{ = }\frac{-2\pm\sqrt[]{4+480}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/u9ebp58uhddxk07r7jtrzuty83n4nn4muf.png)
Continuing the calculos, we find:
![x=\frac{-2\pm\sqrt[]{484}}{2}=\text{ }(-2\pm22)/(2)](https://img.qammunity.org/2023/formulas/mathematics/college/87ullvfw8lqk5mtlaohc1779k64q92ve4n.png)
So, our x can be:
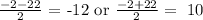
We want the positive solution, so our integers are 10 and 12.