Question

The product of two consecutive positive even integers is 120. Find the integers.

Answer 1

The question says that the product of two consecutives even integers is 120, wich give us the expression:

`x(x+2)=120`

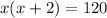
Developing the calculations, we end with the followed second degree equation:

`x^2\text{ + 2x = 120 }\Rightarrow\text{ x}^2\text{ + 2x - 120=0}`

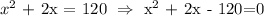
We can use Bhaskara's formula to find the roots, as follow:

`x=\frac{-2\pm\sqrt[]{2^2-4(1)(-120)}}{2*1}\text{ = }\frac{-2\pm\sqrt[]{4+480}}{2}`

Continuing the calculos, we find:

`x=\frac{-2\pm\sqrt[]{484}}{2}=\text{ }(-2\pm22)/(2)`

So, our x can be:

`(-2-22)/(2)\text{ = -12 or }(-2+22)/(2)=\text{ 10}`

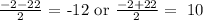
We want the positive solution, so our integers are 10 and 12.