The recursive formula is
a = 57 ------- first term and d = -3 ------- common difference
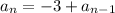
The explicit formula of the sequence is
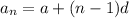
Where d is the constant difference between each 2 consecutive terms
∵ a is the first term
∴ a = 57
∵ d is the constant difference
∴ d = -3
→ Substitute them in the form above
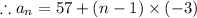
Let us simplify it
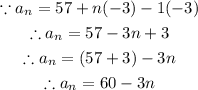
Then the explicit formula is an = 60 - 3n