Question

Given that f(x) is continuous, ƒ²ƒx)dx =7, ƒ^ƒ(x)dx =−3, and ƒª½‚ƒx)dx = 2.Then (x)dx =I have the multiple choice responses

Answer 1

We are given a set of definite integrals and we are tasked to find the area of the curve from x = 0 to 2.

To do this, we need to recall the adding intervals rules for definite integrals:

`\int_a^bf(x)dx+\int_b^cf(x)dx=\int_a^cf(x)dx`

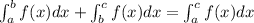
Plugging in the given, we have the following equation:

`\begin{gathered} \int_(-2)^2f(x)dx+\int_0^4f(x)dx-\int_0^2f(x)dx=\int_(-2)^4f(x)dx \\ \\ 7+(-3)-\int_0^2f(x)dx=2 \\ \\ -\int_0^2f(x)dx=-2 \\ \\ \int_0^2f(x)dx=2 \end{gathered}`

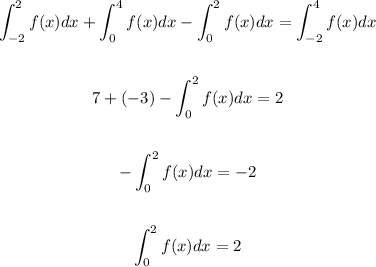
The answer is 2.