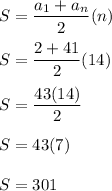Answer: S=301
Explanation:
2 + 5 + 8 + ... +41
The difference of an arithmetic progression:
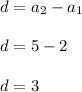
Any (nth) term of the progression can be calculated using the formula for the total term:
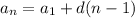
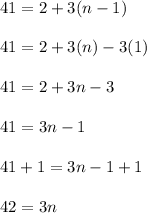
Divide both parts of the equation by 3:
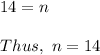
The sum of all the members of an arithmetic progression is equal to half the product of the sum of its outermost members by the number of all its members. where S is the sum of all the members, a₁ is the first member of the progression, an is the last member, and n is the number of members in the given progression: