Vectors u and v are shown in the graph. What is projvu?

Question

asked Nov 28, 2023 38.7k views

1 Answer

Stephen Blum · Answer 1 · 2023-12-02T02:56:51+0000

In order to calculate the projection of u on v, we can use the formula below:

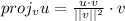
$proj_vu=(u\cdot v)/(||v||^2)\cdot v$

First, let's define the vectors u and v from the image:

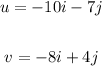
$\begin{gathered} u=-10i-7j\\ \\ v=-8i+4j \end{gathered}$

Now, let's calculate the dot product on the numerator:

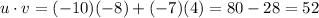
$u\cdot v=(-10)(-8)+(-7)(4)=80-28=52$

The denominator can be calculated as the dot product of v and itself:

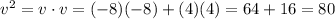
$v^2=v\cdot v=(-8)(-8)+(4)(4)=64+16=80$

Therefore the projection is given by:

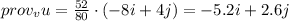
$prov_vu=(52)/(80)\cdot(-8i+4j)=-5.2i+2.6j$

Correct option: the second one.