Question

the velocity function, in feet per second, is given for a particle moving along a straight line, where t is the time in seconds. Findthe displacement andthe total distance that the particle travels over the given interval.

Answer 1

When given a displacement function, its derivative is the velocity function. Vice versa, when given a velocity function, its integral is the displacement function.

So, we need to integrate the given function to find the displacement function.

`\begin{gathered} \int(t^3-8t^2+15t)dt \\ \\ =\int t^3dt-\int8t^2dt+\int15tdt \\ \\ =\int t^3dt-8\int t^2dt+15\int tdt \\ \\ =(t^4)/(4)-8((t^3)/(3))+15((t^2)/(2))+C \\ \\ =(t^4)/(4)-(8t^3)/(3)+(15t^2)/(2)+C \end{gathered}`

To solve for C, we need to have a known displacement. We know that when t = 0, the object has not moved yet. Therefore, it is safe to assume that d must be 0.

`\begin{gathered} (t^4)/(4)-(8t^3)/(3)+(15t^2)/(2)+C=0 \\ \\ (0^4)/(4)-(8(0^3))/(3)+(15(0^2))/(2)+C=0 \\ \\ C=0 \end{gathered}`

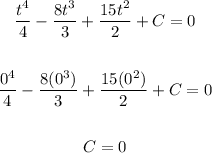
So now we know that the displacemnet function is:

`d(t)=(t^(4))/(4)-(8t^(3))/(3)+(15t^(2))/(2)`

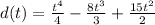
We can now solve for the total displacement when t = 5.

`\begin{gathered} d(t)=(t^(4))/(4)-(8t^(3))/(3)+(15t^(2))/(2) \\ \\ d(5)=(5^4)/(4)-(8(5^3))/(3)+(15(5^2))/(2) \\ \\ d(5)=(625)/(4)+(1,000)/(3)+(375)/(2) \\ \\ d(5)=(8,125)/(12)\approx677.083 \end{gathered}`

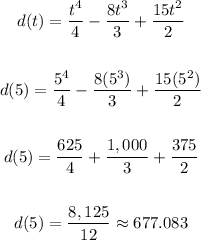
Therefore, the total displacement is 677.083 feet.

Because the particle is moving along a straight line, then the distance is equal to the displacement.