SOLUTION
The radius of the cone is half the radius of the cylinder.
Let r be the radius of cylinder
Then the radius of cone is

The height of the cone is equal to the radius of the cylinder
Hence the height of the cone is
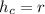
The formula for volume of a cone is given as:
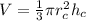
Substitute the radius and height of cone into the formula
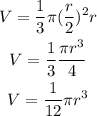
Therefore the required volume is