Question

After 15 yr there will be ? g of a radioactive substance

Answer 1

After 15 years, there will be 3.150 grams of substance.

Explanation:

Remember that the general exponential function for decay is:

`Q(t)=Q_0e^(kt)`

Where Q(t) is the quantity after t years, and Qo is the initial quantity.

Since we know that there were 10 grams initially and that after 9 years only 5 grams remain, we can say that:

`5=10e^(9k)`

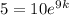
Solving for k,

`\begin{gathered} 5=10e^(9k) \\ \rightarrow(5)/(10)=e^(9k) \\ \\ \rightarrow0.5=e^(9k)\rightarrow\ln(0.5)=9k \\ \\ \Rightarrow k=(\ln(0.5))/(9) \end{gathered}`

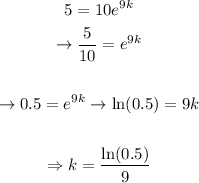
This way, we'll have that:

`Q(t)=10e^{(\ln(0.5))/(9)t}`

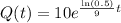
We can calculate how much substance is left after 15 years as following:

We can conclude that after 15 years, there will be 3.150 grams of substance.