Question

Two concentric circles are shown. The length of the arc MN is 37 cm and the length of the arc RE is 67 cm30АWhich statements are correct? Select all that apply.The radius of the larger circle is 18 cm.The radius of the smaller circle is 18 cm.The length of the segment NE is 9 cm.The length of the segment MR is 18 cm.The circumference of the larger circle is 727 cm.The circumference of the larger circle is 367 cm.SUBMIT AND CONTINGO BACK8122

Answer 1

Given:

`\begin{gathered} \text{length of arc MN = 3}\pi cm \\ \text{length of arc }RE\text{ = }6\pi cm \\ \text{angle subtended at the center = }30 \end{gathered}`

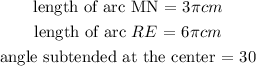
The subtended by both arcs is the same

From the length of arc formula:

`\text{length of arc = }(\theta)/(360)\text{ }*\text{ 2}\pi r`

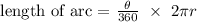
Let us walk through the options to check which is correct

Radius of the larger circle:

`\begin{gathered} r\text{ = }\frac{l*\text{ 360}}{\theta\text{ }*\text{ 2}\pi} \\ =\text{ }\frac{6\pi\text{ }*\text{ 360}}{30\text{ }*\text{ 2}\pi} \\ =\text{ 36 }cm \end{gathered}`

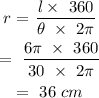
Radius of the smaller circle:

`\begin{gathered} r\text{ = }\frac{l*\text{ 360}}{\theta\text{ }*\text{ 2}\pi} \\ =\text{ }\frac{3\pi\text{ }*\text{ 360}}{30\text{ }*\text{ 2}\pi} \\ =\text{ 18 }cm \end{gathered}`

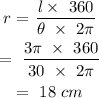
The length of the segment NE:

This is difference between the radius of the larger circle and that of the smaller circle:

`\begin{gathered} =\text{ }36\text{ - 18} \\ =\text{ 18 }cm \end{gathered}`

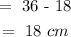
The length of the segment MR:

This is difference between the radius of the larger circle and that of the smaller circle:

`\begin{gathered} =\text{ 36 - 18} \\ =\text{ 18 }cm \end{gathered}`

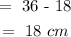
The circumference of the larger circle:

`\begin{gathered} =\text{ 2}\pi r \\ =\text{ 2 }*\text{ }\pi\text{ }*\text{ 36} \\ =\text{ 72}\pi cm \end{gathered}`

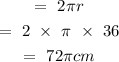
Hence, the statements that are correct are:

Statement 2

Statement 4

Statement 5