Question

(Algebra)A boat traveled a combined total of 476 miles during a trip downstream and back. The trip downstream took 14 hours. The trip back took 34 hours. Find the speed of the current in miles per hour. (hint: the speed of the boat while going downstream is the boat, B, plus the current, C)

Answer 1

Given,

The total distance travelled is 476 miles.

The time taken by the boat for upstream is 14 hours.

The time taken by the boat for downstream is 34 hours.

Consider, The speed of the boat is B miles/hour.

The speed of the current is C miles/hour.

The speed at downstream is B+C miles/hour.

The speed at upstream is B-C miles/hour.

The formula of speed is,

`\begin{gathered} \text{Speed}=(Dis\tan ce)/(time) \\ \end{gathered}`

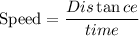
For downstream,

`\begin{gathered} B+C=(476)/(14) \\ B+C=34\text{ miles/hour}\ldots\ldots\ldots(1) \end{gathered}`

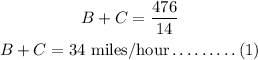
For upstream,

`\begin{gathered} B-C=(476)/(34) \\ B-C=14\text{ miles/hour}\ldots\ldots\ldots(2) \end{gathered}`

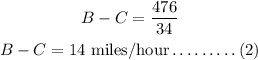
Adding equation (1) and equation (2) then,

`\begin{gathered} B+C+B-C=34+14 \\ 2B=48 \\ B=24\text{ miles/hour} \end{gathered}`

Substituting the value of B in equation (2),

`\begin{gathered} 24-C=14\text{ miles/hour} \\ C=10\text{miles/hour} \end{gathered}`

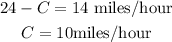
Hence, the speed of current is 10 miles/hour and speed of boat is 24 miles/hour.