Question

f(x) and g(x) are inverses of each other. f(-2) = 13. What is g(13)?Ag(13) = -3Bg(13) = 13Cg(13) cannot be determinedg(13) = -2

Answer 1

We have two functions f ( x ) and g ( x ) unknown to us.

We are given a mapped value of function f ( x ) as follows:

`f\text{ ( -2 ) = 13}`

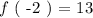
We are given that f ( x ) and g ( x ) are inverses of each other!

Recall, that an inverse of a function is reflection of given function about the following line:

`y\text{ = x}`

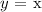
Where,

Whenever we take out inverse of a function every input value ( x ) and the corresponding output of the function are interchanged with one another. This is expressed by the reflection about line ( y = x ).

So for the given data we have:

`x\text{ = -2 , y = 13 : f ( x )}`

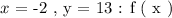
Since, g ( x ) is an inverse of f ( x ). We will interchange each value of x with each value of y. So for the above case we will express:

`x=13,y=-2\colon g(x)=f^{-1\text{ }}\text{ ( x )}`

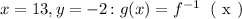
Then the corresponding value for the function g ( x ) would be:

`\begin{gathered} g(13)=f^(-1)\text{ ( 13 ) = -2} \\ \textcolor{#FF7968}{g}\text{\textcolor{#FF7968}{ ( 13 ) = -2}} \end{gathered}`

Answer: Option D